Arus listrik adalah banyaknya muatan listrik yang disebabkan dari pergerakan elektron-elektron, mengalir melalui suatu titik dalamsirkuit listrik tiap satuan waktu. Arus listrik dapat diukur dalam satuan Coulomb/detik atau Ampere. Contoh arus listrik dalam kehidupan sehari-hari berkisar dari yang sangat lemah dalam satuan mikroAmpere ( ) seperti di dalam jaringan tubuh hingga arus yang sangat kuat 1-200 kiloAmpere (kA) seperti yang terjadi pada petir. Dalam kebanyakan sirkuit arus searah dapat diasumsikan resistansi terhadap arus listrik adalah konstan sehingga besar arus yang mengalir dalam sirkuit bergantung padavoltase dan resistansi sesuai dengan hukum Ohm.
) seperti di dalam jaringan tubuh hingga arus yang sangat kuat 1-200 kiloAmpere (kA) seperti yang terjadi pada petir. Dalam kebanyakan sirkuit arus searah dapat diasumsikan resistansi terhadap arus listrik adalah konstan sehingga besar arus yang mengalir dalam sirkuit bergantung padavoltase dan resistansi sesuai dengan hukum Ohm.
 ) seperti di dalam jaringan tubuh hingga arus yang sangat kuat 1-200 kiloAmpere (kA) seperti yang terjadi pada petir. Dalam kebanyakan sirkuit arus searah dapat diasumsikan resistansi terhadap arus listrik adalah konstan sehingga besar arus yang mengalir dalam sirkuit bergantung padavoltase dan resistansi sesuai dengan hukum Ohm.
) seperti di dalam jaringan tubuh hingga arus yang sangat kuat 1-200 kiloAmpere (kA) seperti yang terjadi pada petir. Dalam kebanyakan sirkuit arus searah dapat diasumsikan resistansi terhadap arus listrik adalah konstan sehingga besar arus yang mengalir dalam sirkuit bergantung padavoltase dan resistansi sesuai dengan hukum Ohm.
Arus listrik merupakan satu dari tujuh satuan pokok dalam satuan internasional. Satuan internasional untuk arus listrik adalahAmpere (A). Secara formal satuan Ampere didefinisikan sebagai arus konstan yang, bila dipertahankan, akan menghasilkan gayasebesar 2 x 10-7 Newton/meter di antara dua penghantar lurus sejajar, dengan luas penampang yang dapat diabaikan, berjarak 1 meter satu sama lain dalam ruang hampa udara.
Untuk arus yang konstan, besar arus  dalam Ampere dapat diperoleh dengan persamaan:
dalam Ampere dapat diperoleh dengan persamaan:
 dalam Ampere dapat diperoleh dengan persamaan:
dalam Ampere dapat diperoleh dengan persamaan:
Sedangkan secara umum, arus listrik yang mengalir pada suatu waktu tertentu adalah:
Dengan demikian dapat ditentukan jumlah total muatan yang dipindahkan pada rentang waktu 0 hingga  melalui integrasi:
melalui integrasi:
 melalui integrasi:
melalui integrasi:
Sesuai dengan persamaan di atas, arus listrik adalah besaran skalar karena baik muatan  maupun waktu
maupun waktu  merupakan besaran skalar.Dalam banyak hal sering digambarkan arus listrik dalam suatu sirkuit menggunakan panah, salah satunya seperti pada diagram di atas. Panah tersebut bukanlah vektor dan tidak membutuhkan operasi vektor. Pada diagram di atas ditunjukkan arus mengalir masuk melalui dua percabangan dan mengalir keluar melalui dua percabangan lain. Karena muatan listrik adalah kekal maka total arus listrik yang mengalir keluar haruslah sama dengan arus listrik yang mengalir ke dalam sehingga
merupakan besaran skalar.Dalam banyak hal sering digambarkan arus listrik dalam suatu sirkuit menggunakan panah, salah satunya seperti pada diagram di atas. Panah tersebut bukanlah vektor dan tidak membutuhkan operasi vektor. Pada diagram di atas ditunjukkan arus mengalir masuk melalui dua percabangan dan mengalir keluar melalui dua percabangan lain. Karena muatan listrik adalah kekal maka total arus listrik yang mengalir keluar haruslah sama dengan arus listrik yang mengalir ke dalam sehingga  . Panah arus hanya menunjukkan arah aliran sepanjang penghantar, bukan arah dalam ruang.
. Panah arus hanya menunjukkan arah aliran sepanjang penghantar, bukan arah dalam ruang.
 maupun waktu
maupun waktu  merupakan besaran skalar.Dalam banyak hal sering digambarkan arus listrik dalam suatu sirkuit menggunakan panah, salah satunya seperti pada diagram di atas. Panah tersebut bukanlah vektor dan tidak membutuhkan operasi vektor. Pada diagram di atas ditunjukkan arus mengalir masuk melalui dua percabangan dan mengalir keluar melalui dua percabangan lain. Karena muatan listrik adalah kekal maka total arus listrik yang mengalir keluar haruslah sama dengan arus listrik yang mengalir ke dalam sehingga
merupakan besaran skalar.Dalam banyak hal sering digambarkan arus listrik dalam suatu sirkuit menggunakan panah, salah satunya seperti pada diagram di atas. Panah tersebut bukanlah vektor dan tidak membutuhkan operasi vektor. Pada diagram di atas ditunjukkan arus mengalir masuk melalui dua percabangan dan mengalir keluar melalui dua percabangan lain. Karena muatan listrik adalah kekal maka total arus listrik yang mengalir keluar haruslah sama dengan arus listrik yang mengalir ke dalam sehingga  . Panah arus hanya menunjukkan arah aliran sepanjang penghantar, bukan arah dalam ruang.
. Panah arus hanya menunjukkan arah aliran sepanjang penghantar, bukan arah dalam ruang.
Rapat arus (bahasa Inggris: current density) adalah aliran muatan pada suatu luas penampang tertentu di suatu titik penghantar.Dalam SI, rapat arus memiliki satuan Ampere per meter persegi (A/m2).[5]
di mana  adalah arus pada penghantar, vektor J adalah rapat arus yang memiliki arah sama dengan kecepatan gerak muatan jika muatannya positif dan berlawan arah jika muatannya negatif, dan dA adalah vektor luas elemen yang tegak lurus terhadap elemen. Jika arus listrik seragam sepanjang permukaan dan sejajar dengan dA maka J juga seragam dan sejajar terhadap dA sehingga persamaan menjadi:
adalah arus pada penghantar, vektor J adalah rapat arus yang memiliki arah sama dengan kecepatan gerak muatan jika muatannya positif dan berlawan arah jika muatannya negatif, dan dA adalah vektor luas elemen yang tegak lurus terhadap elemen. Jika arus listrik seragam sepanjang permukaan dan sejajar dengan dA maka J juga seragam dan sejajar terhadap dA sehingga persamaan menjadi:
 adalah arus pada penghantar, vektor J adalah rapat arus yang memiliki arah sama dengan kecepatan gerak muatan jika muatannya positif dan berlawan arah jika muatannya negatif, dan dA adalah vektor luas elemen yang tegak lurus terhadap elemen. Jika arus listrik seragam sepanjang permukaan dan sejajar dengan dA maka J juga seragam dan sejajar terhadap dA sehingga persamaan menjadi:
adalah arus pada penghantar, vektor J adalah rapat arus yang memiliki arah sama dengan kecepatan gerak muatan jika muatannya positif dan berlawan arah jika muatannya negatif, dan dA adalah vektor luas elemen yang tegak lurus terhadap elemen. Jika arus listrik seragam sepanjang permukaan dan sejajar dengan dA maka J juga seragam dan sejajar terhadap dA sehingga persamaan menjadi:
maka
di mana  adalah luas penampang total dan
adalah luas penampang total dan  adalah rapat arus dalam satuan A/m2.
adalah rapat arus dalam satuan A/m2.
Contoh Soal Hukum Kirchhoff 1
Contoh Soal Hukum Kirchhoff
 adalah luas penampang total dan
adalah luas penampang total dan  adalah rapat arus dalam satuan A/m2.
adalah rapat arus dalam satuan A/m2.Pengertian dan Bunyi Hukum Kirchhoff 1
Hukum Kirchhoff 1 merupakan Hukum Kirchhoff yang berkaitan dengan dengan arah arus dalam menghadapi titik percabangan. Hukum Kirchhoff 1 ini sering disebut juga dengan Hukum Arus Kirchhoff atau Kirchhoff’s Current Law (KCL).
Bunyi Hukum Kirchhoff 1 adalah sebagai berikut :
“Arus Total yang masuk melalui suatu titik percabangan dalam suatu rangkaian listrik sama dengan arus total yang keluar dari titik percabangan tersebut.”
Untuk lebih jelas mengenai Bunyi Hukum Kicrhhoff 1, silakan lihat rumus dan rangkaian sederhana dibawah ini :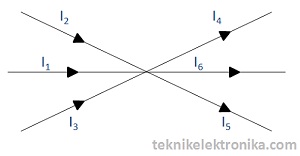

Berdasarkan Rangkaian diatas, dapat dirumuskan bahwa :
I1 + I2 + I3 = I4 + I5 + I6
Contoh Soal Hukum Kirchhoff 1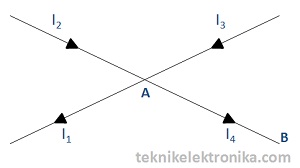
Dari rangkaian diatas, diketahui bahwa
I1 = 5A
I2 = 1A
I3 = 2A
I2 = 1A
I3 = 2A
Berapakah I4 (arus yang mengalir pada AB) ?
Penyelesaian :
Dari gambar rangkaian yang diberikan diatas, belum diketahui apakah arus I4 adalah arus masuk atau keluar. Oleh karena itu, kita perlu membuat asumsi awal, misalnya kita mengasumsikan arus pada I4 adalah arus keluar.
Jadi arus yang masuk adalah :
I2 + I3 = 1 + 2 = 3A
Arus yang keluar adalah :
I1 + I4 = 5 + I4
3 = 5 + I4
I4 = 3 – 5
I4 = -2
I1 + I4 = 5 + I4
3 = 5 + I4
I4 = 3 – 5
I4 = -2
Karena nilai yang didapatkan adalah nilai negatif, ini berbeda dengan asumsi kita sebelumnya, berarti arus I4 yang sebenarnya adalah arus masuk.
Pengertian dan Bunyi Hukum Kirchhoff 2
Hukum Kirchhoff 2 merupakan Hukum Kirchhoff yang digunakan untuk menganalisis tegangan (beda potensial) komponen-komponen elektronika pada suatu rangkaian tertutup. Hukum Kirchhoff 2 ini juga dikenal dengan sebutan Hukum Tegangan Kirchhoff atau Kirchhoff’s Voltage Law (KVL).
Bunyi Hukum Kirchhoff 2 adalah sebagai berikut :
“Total Tegangan (beda potensial) pada suatu rangkaian tertutup adalah nol”
Untuk lebih jelas mengenai Bunyi Hukum Kirchhoff 2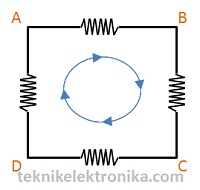 , silakan lihat rumus dan rangkaian sederhana dibawah ini :
, silakan lihat rumus dan rangkaian sederhana dibawah ini :
 , silakan lihat rumus dan rangkaian sederhana dibawah ini :
, silakan lihat rumus dan rangkaian sederhana dibawah ini :
Berdasarkan Rangkaian diatas, dapat dirumuskan bahwa :
Vab + Vbc + Vcd + Vda = 0
Contoh Soal Hukum Kirchhoff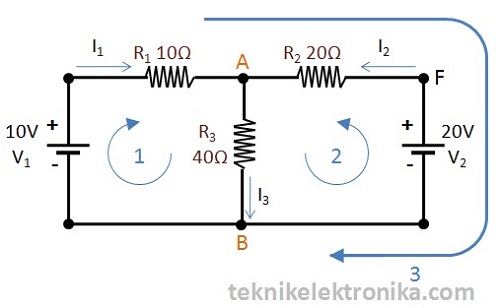
Perhatikan rangkaian diatas, nilai-nilai Resistor yang terdapat di rangkaian adalah sebagai berikut :
R1 = 10Ω
R2 = 20Ω
R3 = 40Ω
V1 = 10V
V2 = 20V
R2 = 20Ω
R3 = 40Ω
V1 = 10V
V2 = 20V
Berakah arus yang melewati resistor R3 ?
Penyelesaian :
Di dalam rangkaian tersebut, terdapat 3 percabangan, 2 titik, dan 2 loop bebas (independent).
Gunakan Hukum Kirchhoff I (Hukum Arus Kirchhoff) untuk persamaan pada titik A dan titik B
Titik A : I1 + I2 = I3
Titik B : I3 = I1 + I2
Titik B : I3 = I1 + I2
Gunakan Hukum Kirchhoff II (Hukum Tegangan Kirchhoff) untuk Loop 1, Loop 2 dan Loop 3.
Loop 1 : 10 = R1 x I1 + R3 x I3 = 10I1 + 40I3
Loop 2 : 20 = R2 x I2 + R3 x I3 = 20I2 + 40I3
Loop 3 : 10 – 20 = 10I1 – 20I2
Loop 2 : 20 = R2 x I2 + R3 x I3 = 20I2 + 40I3
Loop 3 : 10 – 20 = 10I1 – 20I2
Seperti yang dikatakan sebelumnya bahwa I3 adalah hasil dari penjumlahan I1 dan I2, maka persamaannya dapat kita buat seperti dibawah ini :
Persamaan 1 : 10 = 10I1 + 40(I1 + I2) = 50I1 + 40I2
Persamaan 2 : 20 = 20I2 + 40(I1 + I2) = 40I1 + 60I2
Persamaan 2 : 20 = 20I2 + 40(I1 + I2) = 40I1 + 60I2
Jadi saat ini kita memiliki 2 persamaan, dari persamaan tersebut kita mendapatkan nilai I1 dan I2sebagai berikut :
I1 = -0.143 Ampere
I2 = +0.429 Ampere
I2 = +0.429 Ampere
Seperti yang diketahui bahwa I3 = I1 + I2
Maka arus listrik yang mengalir pada R3 adalah -0.143 + 0.429 = 0.286 AmpereSedangkan Tegangan yang melewati R3 adalah 0.286 x 40 = 11.44 Volt
Maka arus listrik yang mengalir pada R3 adalah -0.143 + 0.429 = 0.286 AmpereSedangkan Tegangan yang melewati R3 adalah 0.286 x 40 = 11.44 Volt
Tanda Negatif (-) pada arus I1 menandakan arah alir arus listrik yang diasumsikan dalam rangkaian diatas adalah salah. Jadi arah alir arus listrik seharusnya menuju ke V1, sehingga V2 (20V) melakukan pengisian arus (charging) terhadap V1.
Pengertian Penyajian Data
Penyajian data merupakan salah satu kegiatan dalam pembuatan laporan hasil penelitian yang telah dilakukan agar dapat dipahami dan dianalisis sesuai dengan tujuan yang diinginkan.
Penyajian data merupakan salah satu kegiatan dalam pembuatan laporan hasil penelitian yang telah dilakukan agar dapat dipahami dan dianalisis sesuai dengan tujuan yang diinginkan.
1. Penyajian Data dalam Bentuk Tabel Frekuensi.
Data dapat kita sajikan dalam bentuk tabel atau daftar. Jika data yang akan disajikan cukup besar maka harus dikelompokan terlebih dahulu, kemudian di susun dalam bentuk tabel yang disebut daftar sebaran frekuensi atau daftar distribusi frekuensi.
a. Daftar Distribusi Frekuensi.
• Daftar Distribusi Frekuensi Data Tunggal.

• Daftar Distribusi Frekuensi Data Kelompok.

Data dapat kita sajikan dalam bentuk tabel atau daftar. Jika data yang akan disajikan cukup besar maka harus dikelompokan terlebih dahulu, kemudian di susun dalam bentuk tabel yang disebut daftar sebaran frekuensi atau daftar distribusi frekuensi.
a. Daftar Distribusi Frekuensi.
• Daftar Distribusi Frekuensi Data Tunggal.

• Daftar Distribusi Frekuensi Data Kelompok.

Beberapa istilah yang penting dalam membuat daftar distribusi frekuensi data berkelompok antara lain sebagai berikut :
a) Kelas interval.
b) Batas kelas.
c) Tepi kelas.
d) Panjang kelas.
e) Titik tengah kelas.
a) Kelas interval.
b) Batas kelas.
c) Tepi kelas.
d) Panjang kelas.
e) Titik tengah kelas.
• Cara menyusun Daftar Distribusi Frekuensi Berkelompok.
Beberapa langkah yang perlu di perhatikan dalam menyusun daftar distribusi frekuensi
berkelompok adalah sebagai berikut :
a) Menentukan nilai data terbesar, Xmaks, dan nilai terkecil , Xmin , kemudian di tentukan jangkauannya (J) dengan rumus :
J = X¬maks – Xmin
b) Menentukan banyaknya kelas interval. Salah satu cara untuk menentukan banyaknya kelas interval (k) dari n buah data adalah berdasarkan aturan Sturgess, yaitu :
K = 1 + 3,3 log n
Pada umumnya di ambil nilai 5 ≤ k ≤ 15, tetapi bila jangkauannya besar di ambil Nilai
k : 10 ≤ k ≤20.
c) Menentukan panjang kelas (c) dengan rumus :
c = J/k
d) Menyusun daftar distribusi frekuensi dengan menetapkan kelas-kelas sehingga nilai statistik minimum termuat dalam kelas interval terendah, tetapi tidak harus sebagai batas bawah kelas. Selanjutnya, menetapkan frekuensi tiap kelas yang dapat di lakukan dengan menggunakan rumus.
Beberapa langkah yang perlu di perhatikan dalam menyusun daftar distribusi frekuensi
berkelompok adalah sebagai berikut :
a) Menentukan nilai data terbesar, Xmaks, dan nilai terkecil , Xmin , kemudian di tentukan jangkauannya (J) dengan rumus :
J = X¬maks – Xmin
b) Menentukan banyaknya kelas interval. Salah satu cara untuk menentukan banyaknya kelas interval (k) dari n buah data adalah berdasarkan aturan Sturgess, yaitu :
K = 1 + 3,3 log n
Pada umumnya di ambil nilai 5 ≤ k ≤ 15, tetapi bila jangkauannya besar di ambil Nilai
k : 10 ≤ k ≤20.
c) Menentukan panjang kelas (c) dengan rumus :
c = J/k
d) Menyusun daftar distribusi frekuensi dengan menetapkan kelas-kelas sehingga nilai statistik minimum termuat dalam kelas interval terendah, tetapi tidak harus sebagai batas bawah kelas. Selanjutnya, menetapkan frekuensi tiap kelas yang dapat di lakukan dengan menggunakan rumus.
b. Daftar Distribusi frekuensi Kumulatif, Frekuensi Relatif, dan Frekuensi Kumulatif relatif.
Daftar Distribusi frekuensi kumulatif dapat di susun dari daftar distribusi frekuensi berkelompok. Terdapat dua jenis frekuensi kumulatif, yaitu kumulatif kurang dari tepi atas (fk ≤ ta) dan frekuensi kumulatif lebih dari tepi bawah (fk ≥ tb).
Contoh : Daftar Distribusi Frekuensi Kumulatif

Daftar Distribusi frekuensi kumulatif dapat di susun dari daftar distribusi frekuensi berkelompok. Terdapat dua jenis frekuensi kumulatif, yaitu kumulatif kurang dari tepi atas (fk ≤ ta) dan frekuensi kumulatif lebih dari tepi bawah (fk ≥ tb).
Contoh : Daftar Distribusi Frekuensi Kumulatif

Setiap frekuensi fi, dalam daftar distribusi frekuensi yang dinyatakan dalam persentase di sebut frekuensi relatif (fr). frekuesi relative dapat di tentukan dengan rumus :
fr = fi /n X 100%
Selanjutnya daftar distribusi frekuensi kumulatif relatif dapat di susun dari daftar distribusi kumulatif. Seperti halnya frekuensi kumulatif, terdapat dua jenis frekuensi kumulatif relatif, yaitu frekuensi kumulatif relatif kurang dari tepi atas (fkr ≤ ta) dan frekuensi kumulatif relatif lebih dari tepi bawah (fkr ≥ tb ). Kedua frekuensi kumulatif relative tersebut dapat di tentukan dengan rumus:
(fkr ≤ ta ) =(fk ≤ ta )/n X 100% (fkr ≥ tb ) =(fk ≥ tb )/n X 100%
fr = fi /n X 100%
Selanjutnya daftar distribusi frekuensi kumulatif relatif dapat di susun dari daftar distribusi kumulatif. Seperti halnya frekuensi kumulatif, terdapat dua jenis frekuensi kumulatif relatif, yaitu frekuensi kumulatif relatif kurang dari tepi atas (fkr ≤ ta) dan frekuensi kumulatif relatif lebih dari tepi bawah (fkr ≥ tb ). Kedua frekuensi kumulatif relative tersebut dapat di tentukan dengan rumus:
(fkr ≤ ta ) =(fk ≤ ta )/n X 100% (fkr ≥ tb ) =(fk ≥ tb )/n X 100%
2. Penyajian Data dalam Bentuk Diagram (Garis, Batang, Lingkaran, Pictogram, Histrogram, dan Polygon).
a. Diagram Garis.
Adalah grafik berupa garis, diperoleh dari beberapa ruas garis yang menghubungkan titik-titik pada bidang bilangan. Pada grafik garis digunakan dua garis yang saling berpotongan. Pada garis horizontal (sumbu-X) ditempatkan bilangan-bilangan yang sifatnya tetap, seperti tahun dan ukuran-ukuran. Pada garis tegak (sumbu-Y) ditempatkan bilangan-bilangan yang sifatnya berubah-ubah.
Contohnya tentang perkembangan volume jumlah kendaraan yang melintasi jalan A dalam kurun waktu pukul 0.00 s/d 19.12

a. Diagram Garis.
Adalah grafik berupa garis, diperoleh dari beberapa ruas garis yang menghubungkan titik-titik pada bidang bilangan. Pada grafik garis digunakan dua garis yang saling berpotongan. Pada garis horizontal (sumbu-X) ditempatkan bilangan-bilangan yang sifatnya tetap, seperti tahun dan ukuran-ukuran. Pada garis tegak (sumbu-Y) ditempatkan bilangan-bilangan yang sifatnya berubah-ubah.
Contohnya tentang perkembangan volume jumlah kendaraan yang melintasi jalan A dalam kurun waktu pukul 0.00 s/d 19.12

b. Diagram Batang
Adalah grafik data berbentuk persegi panjang yang lebarnya sama dan dilengkapi dengan skala atau ukuran sesuai dengan data yang bersangkutan. Setiap batang tidak boleh saling menempel atau melekat antara satu dengan lainnya dan jarak antara setiap batang yang berdekatan harus sama.
Ada berbagai bentuk, yaitu: Grafik batangan tunggal (single bar chart), Yaitu grafik yang terdiri dari satu batangan untuk menggambarkan perkembangan (trend) dari suatu karakteristik. Grafik batangan berganda (multiple bar chart), Yaitu grafik yang terdiri dari beberapa garis untuk menggambarkan beberapa hal/kejadian sekaligus.

Adalah grafik data berbentuk persegi panjang yang lebarnya sama dan dilengkapi dengan skala atau ukuran sesuai dengan data yang bersangkutan. Setiap batang tidak boleh saling menempel atau melekat antara satu dengan lainnya dan jarak antara setiap batang yang berdekatan harus sama.
Ada berbagai bentuk, yaitu: Grafik batangan tunggal (single bar chart), Yaitu grafik yang terdiri dari satu batangan untuk menggambarkan perkembangan (trend) dari suatu karakteristik. Grafik batangan berganda (multiple bar chart), Yaitu grafik yang terdiri dari beberapa garis untuk menggambarkan beberapa hal/kejadian sekaligus.

c. Diagram Lingkaran.
Yaitu grafik yang menggambarkan perbandingan nilai-nilai dari suatu karakteristik. Untuk mengetahui perbandingan suatu data terhadap keseluruhan, suatu data lebih tepat disajikan dalam bentuk diagram lingkaran. Grafik data berupa lingkaran yang telah dibagi menjadi juring-juring sesuai dengan data tersebut. Bagian-bagian dari keseluruhan data tersebut dinyatakan dalam persen atau derajat.

Yaitu grafik yang menggambarkan perbandingan nilai-nilai dari suatu karakteristik. Untuk mengetahui perbandingan suatu data terhadap keseluruhan, suatu data lebih tepat disajikan dalam bentuk diagram lingkaran. Grafik data berupa lingkaran yang telah dibagi menjadi juring-juring sesuai dengan data tersebut. Bagian-bagian dari keseluruhan data tersebut dinyatakan dalam persen atau derajat.

d. Diagram Pictogram.
Pictogram adalah bentuk penyajian data statistika dalam bentuk gambar-gambar. Gambar yang digunakan disesuaikan dengan objek yang dideskripsikan yang digunakan untuk mewakili sejumlah objek

Pictogram adalah bentuk penyajian data statistika dalam bentuk gambar-gambar. Gambar yang digunakan disesuaikan dengan objek yang dideskripsikan yang digunakan untuk mewakili sejumlah objek

e. Diagram Histogram.
Penyajian distribusi frekuensi menggunkan gambar yang berbentuk diagram batang tegak. Antara dua bantang yang berdampingan tidak terdapat jarak lebar batang merupakan lebar interval di mulai dari tepi bawah sampai tepi atas interval.
Tepi Bawah = Batas Bawah – 0.5
Tepi Atas = Batas Atas + 0.5

Penyajian distribusi frekuensi menggunkan gambar yang berbentuk diagram batang tegak. Antara dua bantang yang berdampingan tidak terdapat jarak lebar batang merupakan lebar interval di mulai dari tepi bawah sampai tepi atas interval.
Tepi Bawah = Batas Bawah – 0.5
Tepi Atas = Batas Atas + 0.5

f. Diagram Polygon.
Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batang-batangnya dihapus, maka akan diperoleh poligon frekuensi. Berdasarkan contoh di atas dapat dibuat poligon frekuensinya seperti gambar berikut ini.





Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batang-batangnya dihapus, maka akan diperoleh poligon frekuensi. Berdasarkan contoh di atas dapat dibuat poligon frekuensinya seperti gambar berikut ini.

Histogram dan Poligon Frekuensi
Data yang telah disusun dalam bentuk tabel distribusi frekuensi dapat disajikan dalam bentuk diagram yang disebut histogram, yaitu diagram kotak yang lebarnya menunjukkan interval kelas, sedangkan batas-batas tepi kotak merupakan tepi bawah dan tepi atas kelas, dan tingginya menunjukkan frekuensi pada kelas tersebut.
Apabila titik-titik tengah sisi atas dari histogram dihubungkan satu sama lain oleh ruas-ruas garis maka diperoleh poligon frekuensi. Untuk lebih memahami mengenai histogram dan poligon frekuensi, perhatikan contoh berikut.
Berikut ini upah karyawan (dalam ribuan rupiah) per minggu dari sebuah perusahaan.

Langkah-langkah dalam membuat histogram dan poligon frekuensi dari tabel distribusi frekuensi di atas adalah sebagai berikut.
- Membuat sumbu datar dan sumbu tegak yang saling berpotongan.
Untuk menyajikan data yang telah disusun dalam tabel distribusi frekuensi menjadi diagram, seperti biasa dipakai sumbu datar untuk menyatakan kelas interval dan sumbu tegak untuk menyatakan frekuensi. - Menyajikan frekuensi pada tabel ke dalam bentuk diagram.
Setelah sumbu datar dan sumbu tegak dibuat pada langkah 1, buat diagram yang menyatakan frekuensi data. Bentuk diagramnya seperti kotak (diagram batang) dengan sisi-sisi dari batang-batang yang berdekatan harus berimpitan. Pada tepi masing-masing kotak/batang ditulis nilai tepi kelas yang diurutkan dari tepi bawah ke tepi atas kelas. (Perhatikan bahwa tepi kelas terbawah adalah 99,5 – 199,5). - Membuat poligon frekuensi.
Tengah-tengah tiap sisi atas yang berdekatan dihubungkan oleh ruas-ruas garis dan titik-titik tengah sisi-sisi atas pada batang pertama dan terakhir di sisi terakhir dihubungkan dengan setengah jarak kelas interval pada sumbu datar. Bentuk yang diperoleh dinamakan poligon frekuensi (poligon tertutup).
Hasil akhir dari histogram dan poligon frekuensi dari tabel distribusi frekuensi di atas dapat dilihat pada gambar berikut.

Ogive
Ogive adalah grafik yang digambarkan berdasarkan data yang sudah disusun dalam bentuk tabel distribusi frekuensi kumulatif. Untuk data yang disusun dalam bentuk tabel distribusi frekuensi kumulatif kurang dari, grafiknya berupa ogive positif, sedangkan untuk data yang disusun dalam bentuk tabel distribusi frekuensi kumulatif lebih dari, grafiknya berupa ogive negatif.
Frekuensi kumulatif kurang dari untuk suatu kelas adalah jumlah frekuensi semua kelas sebelum kelas tersebut dengan frekuensi kelas itu. Sedangkan frekuensi kumulatif lebih dari suatu kelas adalah jumlah frekuensi semua kelas sesudah kelas tersebut dengan frekuensi kelas itu.
Data upah karyawan sebelumnya dapat digambarkan ogivenya. Akan tetapi sebelum itu, buat terlebih dahulu tabel distribusi frekuensi kumulatifnya.

Dari tabel distribusi frekuensi kumulatif di atas, dapat digambarkan ogive seperti pada diagram berikut.

1. Tabel Distribusi Frekuensi:
a. Distribusi Frekuensi Bergolong
Tabel distribusi frekuensi bergolong biasa digunakan untuk menyusun data yang memiliki kuantitas yang besar dengan mengelompokkan kedalam interval-interval kelas yang sama panjang.
Menurut Viska (2012), langkah-langkah membuat tabel distribusi frekuensi adalah:
1. Urutkan dahulu data, dari data yang terkecil sampai terbesar. Temukan data terkecil dan data terbesarnya.
2. Hitung Jarak atau Rentangan (R)
3. Hitung Jumlah Kelas (K) dengan aturan Sturges
5. Tentukan Batas data terendah atau ujung bawah interval kelas pertama, lalu hitung kelas intervalnya dengan cara: 
6. Kalau sudah, lalu buat tabelnya dengan cara memasukkan nilai interval kelas yang sudah dihitung pada langkah ke-5, dan cari berapa banyak data atau nilai yang sesuai dengan interval kelas tersebut, lalu banyaknya data atau nilai tersebut dimasukkan ke dalam kolom Frekuensi.
Contoh :
Hasil Tugas Matematika dari 40 siswa kelas XI ,berikut ini:
66 75 74 72 79 78 75 75 79 71
75 76 74 73 71 72 74 74 71 70
74 77 73 73 70 74 72 72 80 70
73 67 72 72 75 74 74 68 69 80
Dari data hasil tugas siswa kelas XI, dapat disajikan sebagai berikut :
hari pertama menceritakan pengalaman selama ramadhan
pada hari pertama berpuasa itu sangat bersemangat tapi kalau udah siang hari sambil menunggu buka puasa itu sudah merasa bosan karna saking menahan haus dan lapar dan semenjak hari ke hari berlalu aktivitas yang saya kerjakan selama bulan ramadhan yaitu menjadi koordinator pondok pasantren al hikmah smk 1 pinrang dan saya pun harus menahan capek yang begitu besar karna saya harus betul betul bekerja keras. setelah hari itu berlalu sampai seminggu saya pun istirahat full sambil menunggu buka puasa dengan baca status bbm, facebook, dan web toon dan tak lupa juga saya harus sholat tarawih.
alhamdulillah semua yg telah saya laksanakan pada bulan ramadhan pun berakhir akhirnya datang pun bulan yaitu idul fitri hari kemenangan bagi semua orang islam setelah berpuasa selama sebulan dan saya dengan keluarga pun melaksanakan sholat dan selepas sholat kami bersiap siap untuk mengunjungi rumah nenek atau keponakan dan makanan favorit saya kalau idul fitri adalah sokko dan kari ayam tapi belum sempurna karna tdk ada kakek yg menemani ku makan karna almarhum kakek sudah meninggal kan kami semua beliau selalu menunggu saya untuk makan bersama dan tak lupa pula THR yang selalu iya berikan kepada sya tapi itu semua sudah masa lalu indah yang telah lewat dan tidak akan kembali saya selalu berdoa untuk kakek disana supaya iya tenang disana dan di tempatkan di orang2 yang beriman disisi ALLAH SWT amiin.
Karya Sastra Adalah penciptaan disampaikan kepada komunikatif tentang maksud penulis untuk tujuan estetika. Karya-karya ini sering mengatakan, baik di pertama atau ketiga orang, dengan plot dan melalui penggunaan berbagai perangkat sastra yang berhubungan dengan waktu mereka.
Bentuk Karya Sastra
Dikenal karya sastra dalam dua bentuk, yaitu fiksi dan nonfiksi. sastra fiksi prosa, puisi, dan drama. Sementara contoh nonfiksi sastra adalah biografi, otobiografi, esai, dan kritik sastra. Menurut Suroto, asmara terbentuk pada pengembangan semua aspek kehidupan para pelaku dalam cerita.
Fungsi Karya Sastra
Ada beberapa fungsi sastra, salah satunya disampaikan oleh amriyan Sukandi adalah untuk mengkomunikasikan ide-ide dan menyalurkan pikiran dan perasaan dari pembuat estetika manusia. Gagasan itu disampaikan melalui mandat yang umumnya ada dalam literatur.
Selain ide, dalam literatur ada juga deskripsi peristiwa, gambar psikologis, dan pemecahan masalah jangkauan dinamis. Hal ini dapat menjadi sumber ide dan inspirasi bagi pembaca. Konflik dan tragedi yang digambarkan dalam karya sastra untuk memberikan kesadaran kepada pembaca bahwa ini bisa terjadi dalam kehidupan nyata dan dialami langsung oleh pembaca.
Kesadaran yang membentuk semacam kesiapan batin untuk mengatasi kondisi sosial yang berlaku dalam masyarakat. Sastra juga berguna untuk pembaca sebagai media hiburan.
Jenis- Jenis Karya Sastra Dan Contohnya
- Puisi/ Sajak
Puisi adalah karya sastra yang terikat oleh bait dan array, kata singkat tapi kaya makna, kata-kata yang tidak pulgar tapi dibungkus dengan kekerasan, baik klise atau tidak klise.
- Pantun
Puisi sebenarnya adalah puisi panjang berasal dari Sumatera, Indonesia, sajak dan puisi terikat oleh garis pada setiap baris, dengan rumus abab. Pada pertama dan kedua baris adalah sampiran, sedangkan baris ketiga dan keempat adalah isi.
- Roman
Adalah fiksi yang menceritakan kisah hidup seorang pemuda dari masa kanak-kanak sampai mati, atau dari bayi sampai dewasa. Roman adalah karya sastra lama. Contoh asmara adalah: berlayar, Siti Nurbaya.
- Novel
Novel adalah bentuk sastra yang menceritakan kisah fiksi kehidupan seseorang yang dianggap mengesankan. Misalnya, hanya memberitahu remaja untuk orang dewasa. Semua karakter dalam novel adalah fiktip belaka, tetapi disesuaikan dengan waktu ketika cerita itu ditulis. Jadi terjadi seolah-olah itu terjadi pada saat itu. Novel ini termasuk sastra modern.
- Cerpen
Cerita pendek cerita pendek pendek, seperti namanya cerita pendek biasanya terdiri dari 2-5 lembar kertas polio atau ukuran F4. Cerita pendek hanya menceritakan peristiwa yang paling berkesan yang menimpa tokoh utama.
- Dongeng
Dongeng adalah cerita lama yang biasanya alias penulis tidak diketahui anonim, mengatakan hanya dari mulut ke mulut. Meskipun kini telah dikumpulkan dalam bentuk tertulis. Di masa lalu sudah kelajiman ketika orang tua menceritakan kisah membuai dia. Sekarang hampir tidak ada orang tua mendongeng kepada anak-anak mereka.
- Legenda
Legenda sebenarnya hampir sama dengan dongeng tidak diketahui siapa penulisnya. Namun legenda mengatakan tempat asal atau kisah kerajaan kuno. Misalnya “Sangkuriang” menceritakan asal-usul Gunung Maras.
- Naskah Drama
Bermain adalah cerita lengkap dengan adegan dan dialog dari karakter. Dalam bermain aktor yang terorganisasi dengan baik cerita tentang bagaimana berbicara dan bagaimana adegan, dan ekspresi di wajahnya. Drama biasanya dimulai dengan prolog. Selain dialog antara para pemain ada juga monolog karakter. Monolog adalah karakter berbicara dengan dirinya sendiri. Bermain A adalah untuk dipentaskan dalam seni pertujukkan drama di dalam gedung dan di atas panggung.









